Organiser le cadre des décalages de jeux de données

Organisation des décalages de jeux de données

Prendre du recul sur les causes de la dégradation du modèle

En collaboration avec Marco Dalla Vecchia en tant que créateur de l’image

Nous entraînons des modèles et les utilisons pour prédire certains résultats en fonction d’un ensemble d’entrées. Nous connaissons tous ce jeu du ML. Nous en savons beaucoup sur leur entraînement, au point qu’ils ont évolué en IA, le plus haut niveau d’intelligence jamais atteint. Mais quand il s’agit de les utiliser, nous ne sommes pas si avancés, et nous continuons d’explorer et de comprendre chaque aspect qui compte une fois que les modèles sont déployés.

Aujourd’hui, nous allons discuter du problème de la dérive des performances du modèle (ou simplement de la dérive du modèle), également fréquemment connue sous le nom d’échec du modèle ou de dégradation du modèle. Ce dont nous parlons, c’est de la qualité des prédictions que notre modèle ML fournit. Que ce soit une classe ou un nombre, nous nous intéressons à l’écart entre cette prédiction et ce que serait la classe réelle ou la valeur réelle. Nous parlons de dérive des performances du modèle lorsque la qualité de ces prédictions diminue par rapport au moment où nous avons déployé le modèle. Vous avez peut-être trouvé d’autres termes pour ce sujet dans la littérature, mais restez avec moi sur la dérive des performances du modèle ou simplement la dérive du modèle, du moins pour l’objet de notre conversation actuelle.

Ce que nous savons

Plusieurs blogs, livres et nombreux articles ont exploré et expliqué les concepts fondamentaux de la dérive du modèle, nous entrerons donc d’abord dans cette image actuelle. Nous avons principalement organisé les idées autour des concepts de dérive covariée, de dérive antérieure et de dérive conditionnelle. Cette dernière est également couramment connue sous le nom de dérive conceptuelle. Ces dérives sont connues pour être les principales causes de la dérive du modèle (rappelez-vous, une baisse de la qualité des prédictions). Les définitions résumées sont les suivantes :

• Au-delà de LLaMA La puissance des LLM ouverts
• Suivez les listes TDS pour découvrir nos meilleurs articles
• L’utilisation de la biométrie comme méthode de cybersécurité

• Dérive covariée : Changements dans la distribution de P(X) sans nécessairement avoir de changements dans P(Y|X). Cela signifie que la distribution des caractéristiques d’entrée change, et certains de ces changements peuvent entraîner une dérive du modèle.
• Dérive antérieure : Changements dans la distribution de P(Y). Ici, la distribution des étiquettes ou de la variable de sortie numérique change. Il est fort probable que si la distribution de probabilité de la variable de sortie change, le modèle actuel aura une grande incertitude sur la prédiction donnée, il peut donc facilement dériver.
• Dérive conditionnelle (alias dérive conceptuelle) : La distribution conditionnelle P(Y|X) change. Cela signifie que, pour une entrée donnée, la probabilité de la variable de sortie a changé. Autant que nous le sachions jusqu’à présent, cette dérive nous laisse généralement très peu de marge pour maintenir la qualité des prédictions. Est-ce vraiment le cas ?

De nombreuses sources recensent des exemples de ces dérives de jeux de données. L’une des principales opportunités de recherche consiste à détecter ces types de dérives sans avoir besoin de nouvelles étiquettes [1, 2, 3]. Des métriques intéressantes ont récemment été publiées pour surveiller les performances de prédiction du modèle de manière non supervisée [2, 3]. Elles sont en effet motivées par les différents concepts de dérives de jeux de données et reflètent assez précisément les changements dans les distributions de probabilité réelles des données. Nous allons donc plonger dans la théorie de ces dérives. Pourquoi ? Parce qu’il y a peut-être un certain ordre que nous pouvons mettre à propos de ces définitions. En les organisant, nous pourrions avancer plus facilement ou simplement comprendre plus clairement cet ensemble de concepts.

Pour ce faire, revenons au début et faisons une lente dérivation de l’histoire. Prenez un café, lisez lentement et restez avec moi. Ou simplement, ne dérivez pas !

Le modèle réel et le modèle estimé

Les modèles ML que nous entraînons tentent de nous rapprocher d’une relation ou d’une fonction réelle, mais inconnue, qui fait correspondre une certaine entrée X à une sortie Y. Nous distinguons naturellement la relation réelle inconnue de celle estimée. Cependant, le modèle estimé est lié au comportement du modèle réel inconnu. C’est-à-dire que si le modèle réel change et que le modèle estimé n’est pas robuste face à ces changements, les prédictions du modèle estimé seront moins précises.

Les performances que nous pouvons surveiller concernent la fonction estimée, mais les causes de la dérive du modèle se trouvent dans les changements du modèle réel.

• Quel est le modèle réel ? Le modèle réel est basé sur la dite distribution conditionnelle P(Y|X). Il s’agit de la distribution de probabilité d’une sortie donnée une entrée.
• Quel est le modèle estimé ? Il s’agit d’une fonction ê(x) qui estime spécifiquement la valeur attendue de P(Y|X=x). Cette fonction est celle liée à notre modèle ML.

Voici une représentation visuelle de ces éléments :

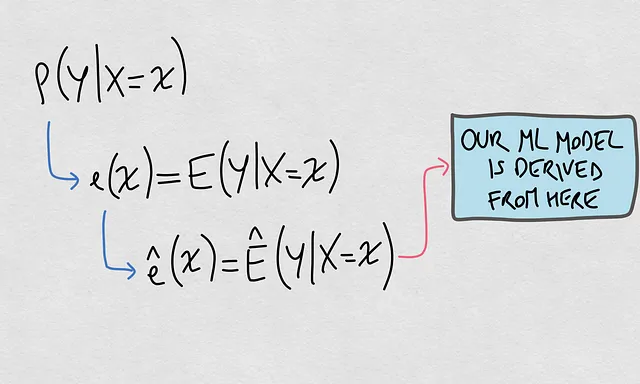
Bien, maintenant que nous avons clarifié ces deux éléments, nous sommes prêts à organiser les idées derrière les soi-disant changements de jeux de données et comment les concepts se connectent entre eux.

Le nouvel agencement

La cause globale de la dérive du modèle

Notre objectif principal est de comprendre les causes de la dérive du modèle pour notre modèle estimé. Parce que nous avons déjà compris la connexion entre le modèle estimé et la distribution de probabilité conditionnelle, nous pouvons affirmer ici ce que nous savions déjà : La cause globale de la dérive de notre modèle estimé est le changement dans P(Y|X).

Basique et apparemment facile, mais plus fondamental que nous le pensons. Nous supposons que notre modèle estimé est un bon reflet du modèle réel. Le modèle réel est régi par P(Y|X). Donc, si P(Y|X) change, notre modèle estimé dérivera probablement. Nous devons être attentifs au raisonnement que nous suivons, comme nous l’avons montré dans la figure ci-dessus.

Nous savions cela déjà auparavant, alors qu’y a-t-il de nouveau à ce sujet ? La nouveauté est que nous baptisons maintenant les changements dans P(Y|X) ici comme la cause globale, et non seulement une cause. Cela imposera une hiérarchie par rapport aux autres causes. Cette hiérarchie nous aidera à positionner les concepts concernant les autres causes de manière appropriée.

Les causes spécifiques : Éléments de la cause globale

Sachant que la cause globale réside dans les changements de P(Y|X), il est naturel de creuser pour savoir quels éléments constituent cette dernière probabilité. Une fois que nous aurons identifié ces éléments, nous continuerons à parler des causes de la dérive du modèle. Alors, quels sont ces éléments ?

Nous le savions toujours. La probabilité conditionnelle est théoriquement définie comme P(Y|X) = P(Y, X) / P(X), c’est-à-dire la probabilité conjointe divisée par la probabilité marginale de X. Mais nous pouvons ouvrir à nouveau la probabilité conjointe et nous obtenons la formule magique que nous connaissons depuis des siècles :

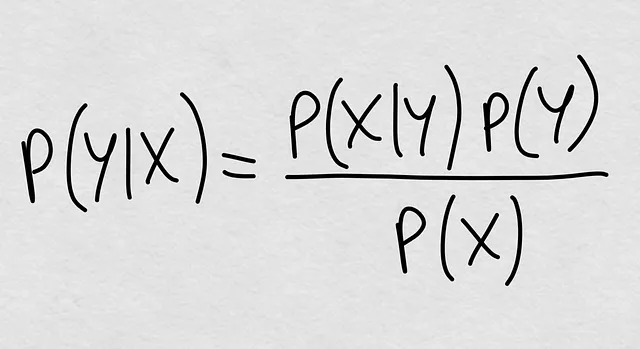
Voyez-vous déjà où nous allons ? La probabilité conditionnelle est quelque chose qui est entièrement défini par trois éléments :

• P(X|Y) : La probabilité conditionnelle inverse
• P(Y) : La probabilité a priori
• P(X) : La probabilité marginale des covariables

Parce que ce sont les trois éléments qui définissent la probabilité conditionnelle P(Y|X), nous sommes prêts à faire une deuxième déclaration : Si P(Y|X) change, ces changements proviennent d’au moins l’un des trois éléments qui le définissent. En d’autres termes, les changements dans P(Y|X) sont définis par tout changement dans P(X|Y), P(Y) ou P(X).

Cela dit, nous avons positionné les autres éléments de nos connaissances actuelles comme des causes spécifiques de la dérive du modèle, plutôt que de simples causes parallèles à P(Y|X).

Revenons au début de cet article, nous avons mentionné le changement de covariables et le changement a priori. Nous notons donc qu’il y a encore une autre cause spécifique : les changements dans la distribution conditionnelle inverse P(X|Y). Nous trouvons généralement une mention de cette distribution lorsqu’il est question des changements dans P(Y), comme si nous considérions de manière générale la relation inverse de Y à X [1,4].

La nouvelle hiérarchie des concepts

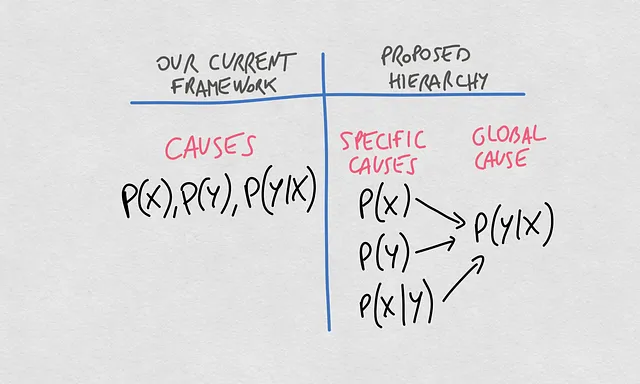
Nous pouvons maintenant faire une comparaison claire entre la pensée actuelle sur ces concepts et la hiérarchie proposée. Jusqu’à présent, nous avons parlé des causes de la dérive du modèle en identifiant différentes distributions de probabilité. Les trois principales distributions, P(X), P(Y) et P(Y|X), sont connues pour être les principales causes de dérive dans la qualité des prédictions renvoyées par notre modèle d’apprentissage automatique.

La nouveauté que je propose ici impose une hiérarchie aux concepts. Dans celle-ci, la cause globale de la dérive d’un modèle qui estime la relation X -> Y est les changements dans la probabilité conditionnelle P(Y|X). Ces changements dans P(Y|X) peuvent provenir de changements dans P(X), P(Y) ou P(X|Y).

Listons certaines des implications de cette hiérarchie :

• Il se peut que P(X) change, mais si P(Y) et P(X|Y) changent également en conséquence, alors P(Y|X) reste le même.
• Il se peut également que P(X) change, mais si P(Y) ou P(X|Y) ne changent pas en conséquence, P(Y|X) changera. Si vous avez déjà réfléchi à ce sujet, vous avez probablement constaté que dans certains cas, nous pouvons voir X changer et ces changements ne semblent pas totalement indépendants de Y|X, donc au final, Y|X change également. Ici, P(X) est la cause spécifique des changements dans P(Y|X), qui à son tour est la cause globale de la dérive de notre modèle.
• Les deux déclarations précédentes sont également vraies pour P(Y).

Étant donné que les trois causes spécifiques peuvent changer ou ne pas changer indépendamment, globalement, les changements dans P(Y|X) peuvent être expliqués par les changements de ces éléments spécifiques dans leur ensemble. Cela peut être parce que P(X) a bougé un peu ici, et P(Y) a bougé un peu là-bas, puis les deux ont également fait changer P(X|Y), ce qui finalement fait changer P(Y|X) dans son ensemble.

Il ne faut pas considérer P(X) et P(Y|X) comme indépendants, P(X) est une cause de P(Y|X)

Où se trouve le modèle d’apprentissage automatique estimé dans tout cela ?

D’accord, maintenant nous savons que les soi-disant variations de covariable et de priorité sont des causes de variation conditionnelle plutôt que parallèles à celle-ci. Les variations conditionnelles englobent l’ensemble des causes spécifiques de la dégradation des performances de prédiction du modèle estimé. Mais le modèle estimé est plutôt une frontière de décision ou une fonction, et non une estimation directe des probabilités en jeu. Alors, que signifient les causes pour les frontières de décision réelles et estimées ?

Réunissons toutes les pièces et dessinons le chemin complet reliant tous les éléments :

Remarquez que notre modèle d’apprentissage automatique peut être obtenu de manière analytique ou numérique. De plus, il peut être représenté de manière paramétrique ou non paramétrique. Ainsi, au final, nos modèles d’apprentissage automatique sont une estimation de la frontière de décision ou de la fonction de régression que nous pouvons déduire de la valeur conditionnelle attendue.

Ce fait a une implication importante pour les causes dont nous avons discuté. Alors que la plupart des changements qui se produisent dans P(X), P(Y) et P(X|Y) impliqueront des changements dans P(Y|X) et donc dans E(Y|X), ils ne signifient pas tous nécessairement un changement dans la frontière de décision ou la fonction réelle. Dans ce cas, la frontière de décision ou la fonction estimée restera valide si celle-ci a été initialement une estimation précise. Regardez cet exemple ci-dessous :

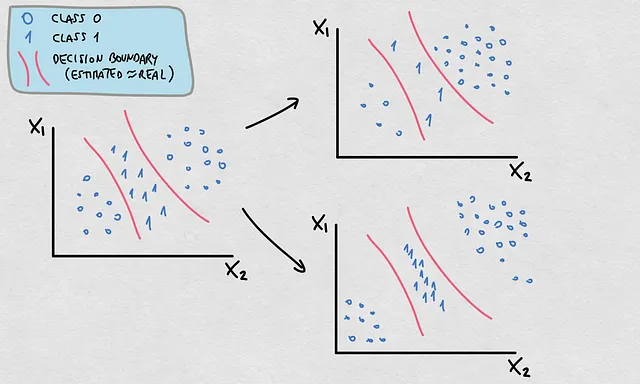
• Remarquez que P(Y) et P(X) ont changé. La densité et l’emplacement des points correspondent à une distribution de probabilité différente
• Ces changements font changer P(Y|X)
• Cependant, la frontière de décision est restée valide

Voici un point important. Imaginons que nous examinions les changements dans P(X) uniquement sans informations sur les étiquettes réelles. Nous aimerions savoir à quel point les prédictions sont bonnes. Si P(X) se déplace vers des zones où la frontière de décision estimée présente une grande incertitude, les prédictions sont probablement inexactes. Ainsi, dans le cas d’une variation de covariable vers des régions incertaines de la frontière de décision, il y a probablement aussi une variation conditionnelle. Mais nous ne saurions pas si la frontière de décision change ou non. Dans ce cas, nous pouvons quantifier un changement qui se produit au niveau de P(X), ce qui peut indiquer un changement dans P(Y|X), mais nous ne saurions pas ce qui se passe avec la frontière de décision ou la fonction de régression. Voici une représentation de ce problème :

Maintenant que nous avons dit tout cela, il est temps pour une autre déclaration. Nous parlons de décalage conditionnel lorsque nous nous référons aux changements dans P(Y|X). Il est possible que ce que nous avons appelé dérive de concept se réfère spécifiquement aux changements dans la frontière de décision réelle ou la fonction de régression. Voici ci-dessous un exemple typique de décalage conditionnel avec un changement dans la frontière de décision mais sans décalage covariable ou antérieur. En fait, le changement est venu du changement dans la probabilité conditionnelle inverse P(X|Y).

Implications pour nos méthodes de surveillance actuelles

Nous nous soucions de comprendre ces causes afin de pouvoir développer des méthodes pour surveiller les performances de nos modèles d’apprentissage automatique aussi précisément que possible. Aucune des idées proposées n’est une mauvaise nouvelle pour les solutions pratiques disponibles. Au contraire, avec cette nouvelle hiérarchie de concepts, nous pourrions être en mesure de pousser plus loin nos tentatives pour détecter les causes de la dégradation des performances des modèles. Nous avons des méthodes et des métriques qui ont été proposées pour surveiller les performances de prédiction de nos modèles, principalement proposées à la lumière des différents concepts que nous avons énumérés ici. Cependant, il est possible que nous ayons mélangé les concepts dans les hypothèses des métriques [2]. Par exemple, nous pourrions avoir fait référence à une hypothèse comme “pas de décalage conditionnel”, quand en réalité il pourrait s’agir spécifiquement de “pas de changement dans la frontière de décision” ou “pas de changement dans la fonction de régression”. Nous devons continuer à réfléchir à cela.

Plus sur la dégradation des performances de prédiction

Zoomer et dézoomer. Nous avons plongé dans le cadre pour réfléchir aux causes de la dégradation des performances de prédiction. Mais nous avons une autre dimension pour discuter de ce sujet, qui concerne les types de décalage des performances de prédiction. Nos modèles souffrent en raison des causes énumérées, et ces causes se reflètent sous la forme de différents types de désalignement de prédiction. Nous trouvons principalement quatre types : biais, pente, variance et décalages non linéaires. Consultez cet article pour en savoir plus sur cet autre aspect de la question.

Résumé

Nous avons étudié dans cet article les causes de la dégradation des performances des modèles et proposé un cadre basé sur les liens théoriques des concepts que nous connaissions déjà. Voici les principaux points :

• La probabilité P(Y|X) régit la frontière de décision ou la fonction réelle.
• La frontière de décision ou la fonction estimée est supposée être la meilleure approximation de la vraie.
• La frontière de décision ou la fonction estimée est le modèle d’apprentissage automatique.
• Le modèle d’apprentissage automatique peut connaître une dégradation des performances de prédiction.
• Cette dégradation est causée par des changements dans P(Y|X).
• P(Y|X) change parce qu’il y a des changements dans au moins un de ces éléments : P(X), P(Y) ou P(X|Y).
• Il peut y avoir des changements dans P(X) et P(Y) sans avoir de changements dans la frontière de décision ou la fonction de régression.

L’énoncé général est le suivant : si le modèle d’apprentissage automatique dérive, alors P(Y|X) change. L’inverse n’est pas nécessairement vrai.

Ce cadre de concepts n’est espérons-le rien d’autre qu’une graine du sujet crucial de la dégradation des performances de prédiction en apprentissage automatique. Bien que la discussion théorique soit simplement un délice, j’ai confiance que cette connexion nous aidera à pousser plus loin l’objectif de mesurer ces changements en pratique tout en optimisant les ressources requises (échantillons et étiquettes). Rejoignez la discussion si vous avez d’autres contributions à apporter à votre connaissance.

Qu’est-ce qui cause la dérive de votre modèle dans les performances de prédiction ?

Bonnes réflexions !

Références

[1] https://huyenchip.com/2022/02/07/data-distribution-shifts-and-monitoring.html

[2] https://www.sciencedirect.com/science/article/pii/S016974392300134X

[3]https://nannyml.readthedocs.io/en/stable/how_it_works/performance_estimation.html#performance-estimation-deep-dive

[4] https://medium.com/towards-data-science/understanding-dataset-shift-f2a5a262a766

We will continue to update IPGirl; if you have any questions or suggestions, please contact us!